Previously I discussed a variant on the harmonic series, $\sum_{n=1}^\infty\cos n/n$. Last time we showed that
\[ \sum_{n=1}^\infty\frac{\cos n}{n} = \sum_{n=1}^\infty\sum_{m=1}^n\cos m\Bigl(\frac{1}{n}-\frac{1}{n+1}\Bigr) , \]
and then showed that the series on the right converges absolutely, by comparison with the series $\sum_{n=1}^\infty3/n^2$.
Since the series on the right converges and the two series have the same value, the series on the left also converges. However, this does not imply that the series on the left also converges absolutely. As a trivial counterexample, if a conditionally convergent series sums to $c$ then $c\sum_{n=1}^\infty \href{http://en.wikipedia.org/wiki/Kronecker_delta}{\delta_{n,1}}$ is an absolutely convergent series which sums to the same value. 🙂
In this post, we answer the question of whether $\sum_{n=1}^\infty\cos n/n$ converges absolutely or not.
First, note that the function $\lvert\cos(x)\rvert+\lvert\cos(x+1)\rvert$ has a positive lower bound (for example, $1/2$), as can be seen from plotting the function:
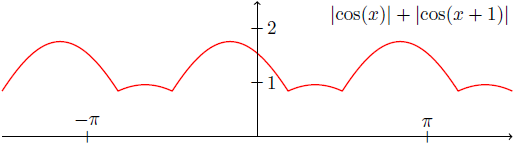
Now, we note that
\[ \frac{\lvert\cos n\rvert}{n} + \frac{\lvert\cos(n+1)\rvert}{n+1} \geq \frac{\lvert\cos(n)\rvert + \lvert\cos(n+1)\rvert}{n+1} \geq \frac{1}{2(n+1)} . \]
Applying this inequality for all odd $n$ and on each two consecutive terms of $\sum_{n=1}^\infty\lvert\cos(n)\rvert/n$ we find that
\begin{align*}
\sum_{n=1}^\infty\frac{\lvert\cos n\rvert}{n} &\geq \sum_{\text{$n$ odd}}\frac{1}{2(n+1)} \\
&= \sum_{n=1}^\infty\frac{1}{2((2n-1)+1)} \\
&= \sum_{n=1}^\infty\frac{1}{4n} = \infty .
\end{align*}
By the comparison test, we find $\sum_{n=1}^\infty\lvert\cos n\rvert/n$ does not converge, and thus $\sum_{n=1}^\infty\cos n/n$ does not converge absolutely.