Previously I discussed the prime number theorem and proved Chebyshev’s weak form of it, namely that $\pi(n)=\Theta(n/\ln n)$. Chebyshev was also able to show the conditional result that if

\[ \lim_{n\to\infty}\frac{\pi(n)}{n/\ln n} \]

exists, then its value is $1$. While this might seem to be quite close to the prime number theorem, there is no especially good reason why the limit should exist. In fact, in a sense this result makes the limit less likely to exist; after our previous proof all one knows is that the limit lies between $0.34$ and $4.16$ (supposing it exists), but now it can have only one possible value!

Some new functions

Before proving this result, it is useful to introduce the von Mangoldt function defined by

\[ \Lambda(n) := \begin{cases}
\ln p & \text{if $n\geq2$ is a perfect power of the prime $p$} \\
0 & \text{otherwise}
\end{cases} \]

and the Chebyshev function defined as the partial sums of the von Mangoldt function,

\[ \psi(n) := \sum_{m\leq n}\Lambda(m) . \]

For each prime $p$ there are $\lfloor\log_p n\rfloor$ perfect powers of $p$ less than or equal to $n$ and strictly greater than $1$, so an alternate way of writing this function is

\[ \psi(n) = \sum_{p\leq n}\lfloor\log_p n\rfloor\ln p . \]

Upper bound on $\psi(n)$

By removing the floor and using the logarithm change-of-base formula one gets an upper bound on $\psi(n)$:

\[ \psi(n) \leq \sum_{p\leq n}(\log_p n)\ln p = \sum_{p\leq n}\ln n = \pi(n)\ln n \]

In particular, using the previously established $\pi(n)=O(n/\ln n)$ this implies

\[ \psi(n) = O(n) . \tag{1} \]

Lower bound on $\psi(n)$

By removing every term in the sum defining $\psi(n)$ except when $m$ is a prime larger than $n’$, and using $\pi(n’)=O(n’/\ln n’)$, one gets a similar lower bound on $\psi(n)$:

\begin{align*}
\psi(n) &\geq \sum_{n'<p\leq n}\ln p \\
&\geq \sum_{n'<p\leq n}\ln n’ \\
&= \ln n’\bigl(\pi(n)-\pi(n’)\bigr) \\
&= \pi(n)\ln n’ + O(n’)
\end{align*}

Now, this holds for all $n'<n$, so take $n’:=n/\ln n$ (it is actually not necessary to ensure that $n’$ is an integer). Then the lower bound becomes

\[ \psi(n) \geq \pi(n)(\ln n-\ln\ln n) + O\Bigl(\frac{n}{\ln n}\Bigr) = \pi(n)\ln(n) + O\Bigl(\frac{n\ln\ln n}{\ln n}\Bigr) . \]

Combining the bounds on $\psi(n)$

Since the error term here is $o(n)$, combining with the upper bound $\psi(n)\leq\pi(n)\ln n$ we get the nice relation

\[ \psi(n) = \pi(n)\ln n + o(n) . \]

Dividing by $n$, we find that

\[ \frac{\psi(n)}{n} = \frac{\pi(n)}{n/\ln n} + o(1) . \tag{2} \]

This is a very strong asymptotic relation between $\psi(n)/n$ and $\pi(n)/(n/\ln n)$; it says that the difference between these functions goes to zero as $n$ increases. So as $n$ gets large, the functions essentially become identical.

The first estimation of $\ln(n!)$

The proof now proceeds by estimating the quantity $\ln(n!)$ in two different ways. The first way is a weak form of Stirling’s approximation:

\[ \ln(n!) = n \ln n + O(n) \tag{3} \]

A simple proof of this proceeds by estimating $\newcommand{\d}{\,\mathrm{d}}\int_1^n\ln t\d t$ by rectangles of width $1$:

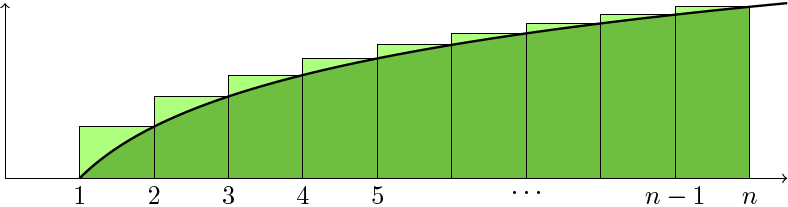
Note that $\ln(n!)=\sum_{m=1}^\infty \ln m$, so the area formed by the rectangles is exactly the quantity to estimate in (3).

As shown in the diagram, this quantity is closely under-estimated by $\int_1^n\ln t\d t$ (the dark green area); the amount of under-estimation is given by the light green area. Although this is difficult to evaluate exactly, by sliding the light green triangle-like shapes to the right they all fit inside the final rectangle, which has area $\ln n$. Thus the dark green area under-estimates the area of the rectangles by at most $\ln n$, and we have

\begin{align*}
\ln(n!) &= \int_1^n\ln t\d t + O(\ln n) \\
&= \bigl[t\ln n – t\bigr]_1^n + O(\ln n) \\
&= n\ln n \mathbin- n + O(\ln n)
\end{align*}

which is a stronger form of (3).

The second estimation of $\ln(n!)$

The second method of estimation relies on the prime factorization of $n!$. Recall we had already determined the exponent of $p$ in the prime factorization (also known as the $p$-adic order) of $n!$ to be $\nu_p(n!) := \sum_{k=1}^\infty\lfloor n/p^k\rfloor$. Using this, we have:

\begin{align*}
\ln(n!) &= \ln\Bigl(\prod_{p\leq n}p^{\nu_p(n!)}\Bigr) \\
&= \sum_{p\leq n}\nu_p(n!)\ln p \\
&= \sum_{p^k\leq n}\biggl\lfloor\frac{n}{p^k}\biggr\rfloor\ln p \\
&= \sum_{m\leq n}\Bigl\lfloor\frac{n}{m}\Bigr\rfloor\Lambda(m) \\
&= \sum_{m\leq n}\Bigl(\frac{n}{m} + O(1)\Bigl)\Lambda(m) \\
&= n\sum_{m\leq n}\frac{\Lambda(m)}{m} + O\bigl(\psi(n)\bigr)
\end{align*}

We can evaluate $\sum_{m\leq n}\Lambda(m)/m$ using a trick known as Abel’s summation formula:

\begin{align*}
\sum_{m\leq n}\frac{\Lambda(m)}{m} &= \sum_{m\leq n}\frac{\psi(m)-\psi(m-1)}{m} \\
&= \sum_{m\leq n}\frac{\psi(m)}{m} \mathbin- \sum_{m\leq n-1}\frac{\psi(m)}{m+1} \\
&= \sum_{m\leq n-1}\psi(m)\Bigl(\frac{1}{m}-\frac{1}{m+1}\Bigr) + \frac{\psi(n)}{n} \\
&= \sum_{m\leq n-1}\psi(m)\Bigl[-\frac{1}{t}\Bigr]_m^{m+1} + \frac{\psi(n)}{n} \\
%&= \sum_{m\leq n-1}\psi(m)\int_m^{m+1}\frac{\!\d t}{t^2} + \frac{\psi(n)}{n} \\
&= \sum_{m\leq n-1}\int_m^{m+1}\frac{\psi(t)}{t^2}\!\d t + \frac{\psi(n)}{n} \\
&= \int_1^n\frac{\psi(t)}{t^2}\!\d t + \frac{\psi(n)}{n}
\end{align*}

Most of this is just algebra; the fact that $\psi(m)=\psi(t)$ for $t\in[m,m+1)$ justifies pulling $\psi(m)$ into the integral. Putting these together and using (1), we get our second estimate on $\ln(n!)$:

\[ \ln(n!) = n\int_1^n\frac{\psi(t)}{t^2}\!\d t + O(n) \tag{4} \]

Putting the estimates together

Combining (3) and (4) and dividing by $n$ we find that

\[ \int_1^n\frac{\psi(t)}{t^2}\!\d t = \ln n + O(1) . \tag{5} \]

Using (5) to derive the result

Suppose that the limit in question exists and equals $1+\epsilon$ for some $\epsilon>0$. Then, taking the limit as $n\to\infty$ in (2), we have

\[ \lim_{n\to\infty}\frac{\psi(n)}{n} = \lim_{n\to\infty}\frac{\pi(n)}{n/\ln n} = 1 + \epsilon . \]

It follows that there is some $N$ such that $\psi(t)/t\geq 1+\epsilon/2$ for all $t\geq N$. Now, $N$ only depends on the constant $\epsilon$, so taking $N$ fixed as $n\to\infty$ we have
\[ \int_1^n\frac{\psi(t)}{t^2}\d t \geq \int_N^n\frac{\psi(t)}{t^2}\d t \geq \int_N^n\frac{1+\epsilon/2}{t}\d t = \Bigl(1+\frac{\epsilon}{2}\Bigr)\ln n + O(1) . \]

This contradicts (5), since the coefficient on the leading term $\ln n$ is larger than $1$; for example, this implies that $\int_1^n\psi(t)/t^2\d t-\ln n=\Omega(\ln n)$, which is not $O(1)$ as given by (5).

Similarly, if the limit in question exists and equals $1-\epsilon$ for some $\epsilon>0$ then we have $\lim_{n\to\infty}\psi(n)/n = 1-\epsilon$, so there exists some $N$ such that $\psi(t)/t\leq1-\epsilon/2$ for all $t\geq N$. Then as $n\to\infty$ we have

\[ \int_1^n\frac{\psi(t)}{t^2}\d t \leq O(1) + \int_N^n\frac{1-\epsilon/2}{t}\d t = \Bigl(1-\frac{\epsilon}{2}\Bigr)\ln n + O(1) , \]

which contradicts (5), since this says that the coefficient on the leading term $\ln n$ is less than $1$.

Therefore, we conclude that if $\lim_{n\to\infty}\pi(n)/(n/\ln n)$ exists it cannot be strictly larger than or strictly less than $1$, so it must be exactly $1$.

Here’s another interesting question regarding the convergence of a series. Does

\[ \sum_{n=1}^\infty\frac{\cos n}{n} \]

converge or diverge?

The question I meant to ask on Sunday was whether $\sum_{m,n=1}^\infty1/(m^2+n^2)^2$ converges or diverges, so I’ll give my solution to that problem now. In fact, the methodology closely resembles the divergence proof I gave for the alternate sum, even though this sum converges.

Since all terms in the sum are positive, the sum either converges absolutely or diverges (the sum cannot be conditionally convergent). In either case the terms of the sum may be rearranged without affecting the convergence. For suppose the sum diverges but converges for some rearrangement: since the terms of the rearranged sum are still positive, the rearranged sum would have to converge absolutely, and therefore converge for all rearrangements, contradicting the supposed diverging arrangement.

Therefore we can rearrange the terms as we please; in particular, we can sort the terms in decreasing order, which has the effect of grouping together all terms of the form $1/k^2$ where $k$ is a sum of two squares. The term $1/k^2$ will appear in the sum once for each solution of $m^2+n^2=k$ in positive integers $m$, $n$.¹

For our purposes it is sufficient to note there are at most $\sqrt{k}$ solutions to $m^2+n^2=k$. This follows since we know that $1\leq m\leq\sqrt{k}$ and for each value of $m$ there is at most one solution; the only possible value of $n$ which could work is $\sqrt{k-m^2}$.

The argument proceeds as follows:

\[ \newcommand{\N}{\mathbb{N}}\begin{align*}
\sum_{m,n\in\N}\frac{1}{(m^2+n^2)^2} &= \sum_{k=2}^\infty\sum_{\substack{m,n\in\N\\m^2+n^2=k}}\frac{1}{k^2} \\
&\leq \sum_{k=2}^\infty\frac{\sqrt{k}}{k^2} \\
&= \sum_{k=2}^\infty\frac{1}{k^{3/2}} \\
&= \zeta(3/2)-1
\end{align*} \]

The final sum converges since it is a $p$-series (truncated). By the comparison test, the sum in question also converges.

Previously I asked if the summation $\sum_{m,n=1}^\infty1/(m^2+n^2)$ converges or diverges. Actually, the I intended the denominator of the summation term to be $(m^2+n^2)^2$. But never mind, let’s solve the problem as given. To do this, we’ll employ the comparison test.

First, note that

\[ m^2+n^2 \leq m^2+2mn+n^2 = (m+n)^2 , \]

so $1/(m^2+n^2)\geq1/(m+n)^2$.

Next, assume the sum converges; since all terms are positive the sum absolutely converges and the terms may be rearranged without affecting its value. In particular, we rearrange the terms in decreasing order, by grouping all terms equal to $1/k^2$ together for each possible value of $k$.

Finally, we use the fact that there are exactly $k-1$ solutions to $m+n=k$ in positive integers $m$, $n$. Putting it all together, the argument goes as follows:

\begin{align*}
\newcommand{\N}{\mathbb{N}}
\sum_{m,n\in\N}\frac{1}{m^2+n^2} &\geq \sum_{m,n\in\N}\frac{1}{(m+n)^2} \\
&= \sum_{k=2}^\infty\sum_{\substack{m,n\in\N\\m+n=k}}\frac{1}{k^2} \\
&= \sum_{k=2}^\infty\frac{k-1}{k^2} \\
&\geq \frac{1}{2}\sum_{k=2}^\infty\frac{1}{k} \\
&= \infty
\end{align*}

The final inequality just uses $k-1\geq k/2$ for $k\geq2$ and we are left with a harmonic series, which diverges. By the comparison test the original sum diverges; this contradicts the assumption that it converges, so the sum really does diverge, as required.

Next up, I’ll show the question I intended to ask: does $\sum_{m,n=1}^\infty1/(m^2+n^2)^2$ converge or diverge?

Here’s another cute math problem. Does

\[ \sum_{m=1}^\infty\sum_{n=1}^\infty\frac{1}{m^2+n^2} \]

converge or diverge? I’ll post my solution in a day or two.

A month ago I posed the problem of showing that a monic $\newcommand{\Z}{\mathbb{Z}}f\in\Z[x]$ is squarefree over $\newcommand{\C}{\mathbb{C}}\C$ if and only if it is squarefree over $\Z$.

One direction is straightforward, although the easiest way to see it is to consider the contrapositive. If $f$ is not squarefree over $\Z$ then its factorization over $\Z$ is of the form $hg^2$ where $h$, $g\in\Z[x]$ and $g$ is nonconstant. Since $f$ can only factor farther in $\C$ it follows that $f$ is also not squarefree over $\C$; in particular any root $\alpha\in\C$ of $g$ will have multiplicity at least $2$ in the factorization of $f$ in $\C$.

Thus if $f$ is squarefree over $\C$ it is also squarefree over $\Z$. Conversely, if $f$ is not squarefree over $\C$ then it has some multiple root $\alpha\in\C$ and its factorization is of the form $k\cdot(x-\alpha)^2$, so $f’=k'(x-\alpha)^2+2(x-\alpha)k$ and $\alpha$ is also a root of $f’$.

Since $f$ and $f’$ are polynomials with integer coefficients with $\alpha$ as a root, the minimal polynomial $g$ of $\alpha$ over $\newcommand{\Q}{\mathbb{Q}}\Q$ divides both $f$ and $f’$. In particular, there must be some $h\in\Q[x]$ such that $f=gh$. Then $f’=g’h+h’g$ and since $g\mid f’$ and $g\mid h’g$ we must have $g\mid g’h$. However, $g\nmid g’$ since $g’$ has a smaller degree than $g$ and is $g’$ is nonzero (as the characteristic of $\Q$ is $0$).

Being a minimal polynomial, $g$ is irreducible, and it is also prime as $\Q[x]$ is a UFD. Thus from $g\mid g’h$ and $g\nmid g’$ we must have $g\mid h$, i.e., $g^2\mid f$ and $f$ is not squarefree over $\Q$. By Gauss’ Lemma the factorization $f=g^2(h/g)$ over $\Q$ may actually be taken to be over $\Z$ (by replacing $g$ and $h$ with their primitive parts), so $f$ is not squarefree over $\Z$, as required.

Note that the requirement that $f$ be monic is necessary (at least, the content of $f$ should be squarefree). For example, if $f:=4$ then $f=2\cdot2$ is not squarefree over $\Z$, but is technically squarefree over $\C$, since $4$ is a unit in $\C$!

Here’s an interesting polynomial property that arose in my recent number theory project.

Let $f$ be a monic polynomial with integer coefficients. Show that $f$ is squarefree over $\mathbb{C}$ if and only if $f$ is squarefree over $\mathbb{Z}$.